Question

A highly selective boarding school will only admit students who place at least 2.5 standard deviations above the mean on a standardized test that has a mean of 200 and a standard deviation of 24. What is the minimum score that an applicant must make on the test to be​ accepted?

Answer 1

260 is the minimum score.

Explanation:

We are given the following information in the question:

Mean, μ = 200

Standard Deviation, σ = 24

We are given that the distribution of test score is a bell shaped distribution that is a normal distribution.

Least marks required for admission in boarding school is 2.5 standard deviations above the mean.

Thus, we can calculate the minimum score as:

`=\mu + 2.5(\sigma)\\=200 + 2.5(24)\\=260`

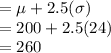
Thus, 260 is the minimum score that an applicant must make on the test to be​ accepted.