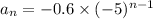Question

Complete the recursive formula of the geometric sequence − 0.6   ,   3   , − 15   ,   75 , . . .

Answer 1

`a_n = -0.6 * (-5)^(n - 1)` is the recursive formula of the geometric sequence

Solution:

Given geometric sequence is:

-0.6, 3 , -15, 75

We have to frame the recursive formula

Find the common ratio

`r = (3)/(-0.6) = -5\\\\r = (-15)/(3) = -5\\\\r = (75)/(-15) = -5`

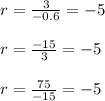
Thus common ratio is -5

The nth term of geometric sequence is given as:

`a_n = a * r^(n-1)`

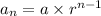
Where,

n is the nth term

a is the first term of sequence

r is common ratio

From sequence,

a = -0.6

r = -5

Therefore,

`a_n = -0.6 * (-5)^(n - 1)`

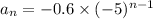
Where, n = 1 , 2 , 3 , 4 , .....

Thus the recursive formula is found