Answer:
(a)
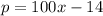
(b)
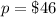
Explanation:
Linear Modeling
It consists of finding an equation of a line that fits the conditions of a certain situation in real life. We'll use a linear model for the cookies of the students.
(a) We know that we have a total of n=100 cookies. If sold for $0.10 each, they lose $4. We have an initial condition (x,p) = (0.10,-4), where x is the price of each cookie and p(x) is the net profit from selling all the cookies. The second conditions are that when then the price is $0.50 each, there is a positive profit of $36, which is a second point (0.5,36). That is enough to build the linear function, that can be found by
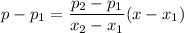

Reducing
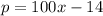
(b) If the students sell the cookies for x=0.60 each, the profit will be
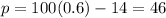
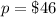
It's a reasonable answer because we have found that increasing the price, the profit will increase also. The model doesn't have any restriction for the price