Question

An Inter City Express train traveling at 250 km/h is

braked to a stop in a distance of 4820 m. If the mass of the
train is 8.63 X 105 kg, what is the average braking force?

Answer 1

F = 431671.31 [N]

Step-by-step explanation:

This problem can be solved using the work and energy theorem, which tells us that the initial mechanical energy (potential energy + kinetic energy) plus the sum of the work from the initial position to the end will be equal to the final mechanical energy.

`E_(M1)+W_(1-2)=E_(M2)\\0.5*m*v_(1)^(2)+W_(1-2)=0.5*m*v_(2)^(2)`

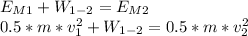
As the train stops at the end, the speed at Point 2 is equal to zero,so we can determine the work, we first convert the speed from [km/h] to meters per second.

`250[(km)/(h)]*1[(h)/(3600s) ]*1000[(m)/(1km) ]\\= 69.44[(m)/(s) ]`

`0.5*(8.63*10^(5))*(69.44)^(2)+W_(1-2)= 0.5*(8.63*10^(5))*(0)^(2)\\W_(1-2)=-2080.66*10^6[J]`

The negative sign means that the work is done in the opposite direction to the movement.

Knowing the work we can calculate the force, since an initial input data is the distance

W = F * d

F = W / d

F = (2080.66*10^6) / 4820

F = 431671.31 [N]