Answer:
431
Explanation:
Let

We want to find the remainder when this polynomial is divided by x+3.
We use the remainder theorem.
Which says that, when p(x) is divided by x-a, the remainder is p(a)=R.
Therefore the remainder when p(x) is divided by x+3 is p(-3).
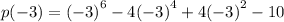
We evaluate:
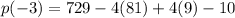
We multiply to get;
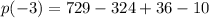
We simplify to get:

Therefore the remainder is 431