Question

A generator uses a coil that has 140 turns and a 0.45-T magnetic field. The frequency of this generator is 60.0 Hz, and its emf has an rms value of 120 V. Assuming that each turn of the coil is a square (an approximation), determine the length of the wire from which the coil is made.

Answer 1

The length of the wire from which the coil is made is 47 m

Step-by-step explanation:

Given;

number of turns, N = 140 turns

magnetic field strength, B = 0.45 T

frequency of the generator, F = 60 Hz

root mean value of emf = 120 V

Peak emf, V₀ = Vrms × √2

V₀ = 120 × √2 = 169.71 V

`L = 4\sqrt{(NV_o)/(B \omega)} \\\\but \ \omega = 2\pi F\\\\L = 4\sqrt{(NV_o)/(2\pi FB)}`

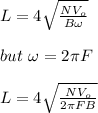
where;

L is the total length of the wire from which the coil is made

substitute the values given and solve for L

`L = 4\sqrt{(NV_o)/(2\pi FB)} \\\\L = 4\sqrt{(140*169.71)/(2\pi *60*0.45)} \ = 4√(140.035) \ = 47 m`

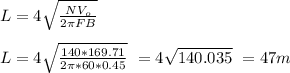
Therefore, the length of the wire from which the coil is made is 47 m