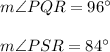Question

In quadrilateral PQRS, Angle P Q R measures (7x - 2)o . Angle PSR measures (5x + 14 )o.

Circle T is inscribed with quadrilateral P Q R S.


What are the measure of angles PQR and PSR?


m Angle P Q R = 54o and m Angle P S R = 54o

m Angle P Q R = 84o and m Angle P S R = 96o

m Angle P Q R = 90o and m Angle P S R = 90o

m Angle P Q R = 96o and m Angle P S R = 84o

Answer 1

m Angle P Q R = 96o and m Angle P S R = 84o

Explanation:

This is the answer 2021 Edge

Hope this Helps!!!!!

Answer 2

Fourth option is correct m Angle P Q R = 96 and m Angle P S R = 84

Therefore,

`m\angle PQR =96\°\\\\m\angle PSR = 84\°`

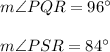
Explanation:

Given:

In quadrilateral PQRS,

∠PQR = (7x - 2)°

∠PSR = (5x + 14)°

Circle T is inscribed with quadrilateral P Q R S.

To Find:

m∠PQR = ?

m∠PSR = ?

Solution:

Circle T is inscribed with quadrilateral P Q R S.

Therefore,

Quadrilateral PQRS is a Cyclic Quadrilateral,

So for a Cyclic Quadrilateral, opposite Angles are Supplementary

∠PQR and ∠PSR are opposite angles

∴
`m\angle PQR+ m\angle PSR =180\°`

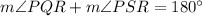
Substituting the values we get

`(7x-2)+(5x+14)=180\\\\12x+12=180\\\\12x=180-12=168\\\\x=(168)/(12)=14`

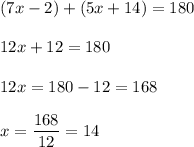
Substitute x in PQR and PSR we get

`m\angle PQR = 7* 14 - 2 =96\°\\\\m\angle PSR = 5* 14 + 14=84\°`

Therefore,

`m\angle PQR =96\°\\\\m\angle PSR = 84\°`