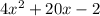If c(x) = 4x – 2 and d(x) = x2 + 5x, what is (cºo)(x)? 4x2 + 18x2 – 10x O x² + 9x-2 16x2 + 4x - 6 O 4x2 + 20x-2

Question

asked Nov 3, 2021 107k views

2 Answers

Paul Lemarchand · Answer 1 · 2021-11-07T08:00:28+0000

Option D:
4x^(2) +20x-2 is the value of
$(c \circ d)(x)$

Step-by-step explanation:

Given that the two functions
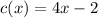c(x)=4 x-2 and
d(x)=x^(2) +5x

To find the value of
$(c \circ d)(x)$ :

The value of
$(c \circ d)(x)$ can be determined using the formula,

$(c \circ d)(x)=c[d(x)]$

First, we shall substitute
d(x)=x^(2) +5x in the above formula.

Thus, we have,

$(c \circ d)(x)=c[x^2+5x]$

Now, substituting
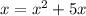x=x^2+5x in the function
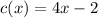c(x)=4 x-2 , we get,

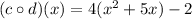
$(c \circ d)(x)=4(x^2+5x)-2$

Simplifying the terms, we get,

$(c \circ d)(x)=4x^2+20x-2$

Therefore, the value of
$(c \circ d)(x)$ is
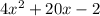
4x^(2) +20x-2

Hence, Option D is the correct answer.