Answer:
Therefore,
 Explanation:
Explanation:
Given:
KP is the angle bisector of ∠ JKL,
∠JKL = 2y + 25
∠ PKL = 8y - 17
To Find:
∠ JKL = ?
Solution:
KP is the angle bisector of ∠ JKL, .. given
Angle bisector divides the angle in two equal parts such that,
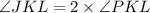
Substituting the values we get
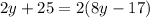
Apply Distributive Property we get
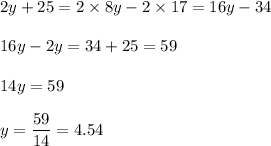
Now substitute y in JKL
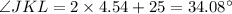
Therefore,
