Question

F(x) = 6x^2+10x-1f(x)=6x

2

+10x−1f, left parenthesis, x, right parenthesis, equals, 6, x, squared, plus, 10, x, minus, 1

What is the value of the discriminant of fff?

How many distinct real number zeros does fff have?

Answer 1

It's just 124 first answer and then two for next.

Answer 2

Therefore,

1. The value of Discriminant of f(x) is

`Discriminant =√(124)`

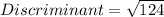
2. f(x) has Two Distinct Real number zeros.

Explanation:

Given:

`f(x)=6x^(2)+10x-1`

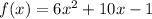
To Find:

1 . What is the value of the discriminant of f(x) = ?

2. How many distinct real number zeros does f(x) have = ?

Solution:

For a Quadratic Equation

`ax^(2)+bx+c=0`

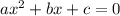
The Discriminant is given as

`Discriminant = \sqrt{b^(2)-4ac}`

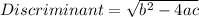
So on Comparing and substituting we get

a = 6 ; b = 10 ; c = -1

Therefore,

`Discriminant = \sqrt{10^(2)-4* 6* -1}=√(124)`

Now if,

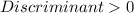`Discriminant > 0` .....f(x) has Two Distinct Real number zeros

here,

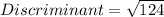`Discriminant =√(124)` Which is greater than zero

Hence f(x) has Two Distinct Real number zeros

Therefore,

1. The value of Discriminant of f(x) is

`Discriminant =√(124)`

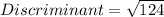
2. f(x) has Two Distinct Real number zeros.