Question

Iron and vanadium both have the BCC crystal structure and V forms a substitutional solid solution for concentrations up to approximately 20 wt% V at room temperature. Compute the unit cell edge length for a 92 wt% Fe-8 wt% V alloy.

Answer 1

The unit cell edge length for the alloy is 0.288 nm

Step-by-step explanation:

Given;

concentration of vanadium, Cv = 8 wt%

concentration of iron, Cfe = 92 wt%

density of vanadium = 6.11 g/cm³

density of iron = 7.86 g/cm³

atomic weight of vanadium, Av = 50.94 g/mol

atomic weight of iron, Afe= 55.85 g/mol

Step 1: determine the average density of the alloy

`\rho _(Avg.) = (100)/((C_v)/(\rho _v) + (C__(Fe))/(\rho _(Fe)) )`

`\rho _(Avg.) = (100)/((8)/(6.11) + (92)/(7.86) ) = 7.68 \ g/cm^3`

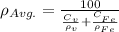
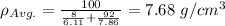
Step 2: determine the average atomic weight of the alloy

`A _(Avg.) = (100)/((C_v)/(A _v) + (C__(Fe))/(A _(Fe)) )`

`A _(Avg.) = (100)/((8)/(50.94) + (92)/(55.85) ) = 55.42 \ g/mole`

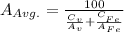
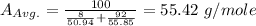
Step 3: determine unit cell volume

`V_c=(nA_(avg.))/(\rho _(avg.) N_a)`

for a BCC crystal structure, there are 2 atoms per unit cell; n = 2

`V_c=(2*55.42)/( 7.68*6.022*10^(23)) = 2.397*10^(-23) \ cm^3/cell`

Step 4: determine the unit cell edge length

Vc = a³

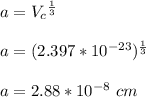`a = V_c{^(1)/(3) }\\\\a = (2.397*10^(-23)}){^(1)/(3)}\\\\a = 2.88 *10^(-8) \ cm`= 0.288 nm

Therefore, the unit cell edge length for the alloy is 0.288 nm