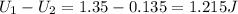Question

A particle (charge 7.5 µC) is released from rest at a point on the x axis, x = 10 cm. It begins to move due to the presence of a 2.0-µC charge which remains fixed at the origin. What is the kinetic energy of the particle at the instant it passes the point x = 1.0 m?

Answer 1

1.215J

Step-by-step explanation:

Using the law of energy conservation, the potential energy is equal to the kinetic energy of the particle during motion:

`U_1=_qV`

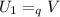
#the V of the 2.0-µC is expressed as:

`V=(1)/(4\pi \epsilon_o r)`

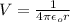
We substitute the given values from the question:

##When the moving charge reaches 0.1meter the energy becomes

`U_1=7.5* 10^(-6)* (2.0*10^(-6))/(4\pi 8.85* 10^(-12)* 0.1\\)\\=1.35J`

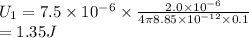
#When the moving charge reaches 1.0 meter the energy becomes

`U_2=7.5* 10^(-6)* (2.0*10^(-6))/(4\pi 8.85* 10^(-12)* 1.0)\\\\=0.135J`

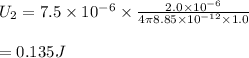
Hence, the change in energy is
`U_1-U_2=1.35-0.135=1.215J`