Answer:
The integers are
5 and 7
Explanation:
Let
x ---> the first consecutive odd integer
x+2 ---> the second consecutive odd integer
we know that
The algebraic expression that represent this situation is
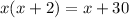
solve for x
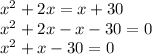
Solve the quadratic equation
The formula to solve a quadratic equation of the form
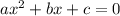
is equal to
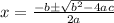
in this problem we have
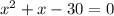
so
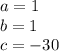
substitute in the formula
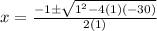
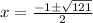
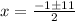
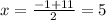
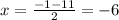 ---> is not a odd integer
---> is not a odd integer
For x=5
The numbers are
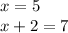
so
5 and 7