Question

Let x be the number of digits in begin math size 16px style 2 to the power of 2001 end style when calculated. Let y be the number of digits in begin math size 16px style 5 to the power of 2001 end style when calculated. Find the sum of x and y

Answer 1

2002

Explanation:

The number of digits in a number is the ceil value of the base-ten logarithm of the number (ceil value means rounding up).

`\text{Number of digits in }N=\left \lceil{\log N}\right \rceil`

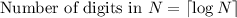
When
`N = 2^(2001)`

`x=\left \lceil{\log 2^(2001)}\right \rceil=\left \lceil{2001\log2} \right \rceil= 603`

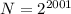
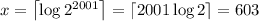
When
`N = 5^(2001)`

`y=\left \lceil{\log 5^(2001)}\right \rceil=\left \lceil{2001\log5} \right \rceil= 1399`

`x+y=603+1399 = 2002`

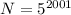
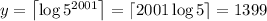
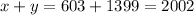
Note that the sum x + y could be derived by finding the number of digits in
`2^(2001)*5^(2001)=10^(2001)`

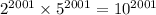
The number of zeros in
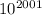`10^(2001)` is 2001. Including the 1 in leftmost digit position gives 2001 + 1 = 2002