The value after 4 years is $ 2244.16
Solution:
The decreasing function is given as:
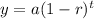
Where,
y is final value
a is initial value
r is decreasing rate in decimal
t is number of years
From given,
a = 3000
t = 4 years
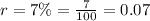
Substituting the values we get,

Thus the value after 4 years is $ 2244.16