Question

Hi:) anyone able to help with 4(a) ? question in the pic attached :) thanks!

Answer 1

Answers:

a = 2

b = -1

====================================================

Work Shown:

`x√(24)+√(96) = √(108)+x√(12)\\\\x√(24)-x√(12) = √(108)-√(96)\\\\x(√(24)-√(12)) = √(108)-√(96)\\\\x = (√(108)-√(96))/(√(24)-√(12))\\\\x = (6√(3)-4√(6))/(2√(6)-2√(3))\\\\`

`x = (3√(3)-2√(6))/(√(6)-√(3))\\\\x = ((3√(3)-2√(6))(√(6)+√(3)))/((√(6)-√(3))(√(6)+√(3))) \text{ rationalizing denominator}\\\\x = (3√(2)-3)/((√(6))^2-(√(3))^2) \text{ see note below; see image attachment below}\\\\x = (3(√(2)-1))/(6-3)\\\\x = (3(√(2)-1))/(3)\\\\x = √(2)-1\\\\`

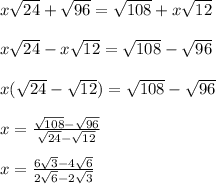
This is in the form
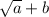`√(a)+b` with a = 2 and b = -1

-----

note: for this line, I expanded each pair of multiplying binomials. In the numerator, I used the box method as shown in the diagram below. Each inner cell is the result of multiplying the corresponding outer cell expressions. Example: for row2, column1, we have
`3√(3) * √(3) = 3√(3*3) = 3√(9) = 3*3 = 9`. The other cells are filled out in a similar fashion. In the denominator, I used the difference of squares rule.