Question

M is a degree 3 polynomial with m ( 0 ) = 53.12 and zeros − 4 and 4 i . Find an equation for m with only real coefficients (i.E. No i in your equation.

Answer 1

Therefore the required polynomial is

M(x)=0.83(x³+4x²+16x+64)

Explanation:

Given that M is a polynomial of degree 3.

So, it has three zeros.

Let the polynomial be

M(x) =a(x-p)(x-q)(x-r)

The two zeros of the polynomial are -4 and 4i.

Since 4i is a complex number. Then the conjugate of 4i is also a zero of the polynomial i.e -4i.

Then,

M(x)= a{x-(-4)}(x-4i){x-(-4i)}

=a(x+4)(x-4i)(x+4i)

=a(x+4){x²-(4i)²} [ applying the formula (a+b)(a-b)=a²-b²]

=a(x+4)(x²-16i²)

=a(x+4)(x²+16) [∵i² = -1]

=a(x³+4x²+16x+64)

Again given that M(0)= 53.12 . Putting x=0 in the polynomial

53.12 =a(0+4.0+16.0+64)

`\Rightarrow a = (53.12)/(64)`

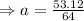
=0.83

Therefore the required polynomial is

M(x)=0.83(x³+4x²+16x+64)