Answer:
The usually speed of the bus is 50 miles/h.
Explanation:
Let the usual speed of the bus be x mile/hour.
We know that
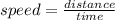
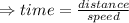
The bus travels 200 miles.
To reach its destination it takes time
 h
h
This week however the bus leaves at 5:40.
The bus late 40 minutes

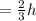
Now the speed of the bus is = (x+10) miles/h
The new time to reach the destination is
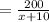 h
h
According to the problem,
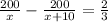
![\Rightarrow 200[(x+10-x)/(x(x+10))]=(2)/(3)](https://img.qammunity.org/2021/formulas/mathematics/high-school/tepapuxiu6l01tj0i7qjpakcvzjpdgr2mf.png)
![\Rightarrow 200[(10)/(x^2+10x)]=(2)/(3)](https://img.qammunity.org/2021/formulas/mathematics/high-school/18u9415vful4r7o4y7kg7gi2iknc30agna.png)
⇒2(x²+10x)=200×10×3
⇒x²+10x = 3000
⇒x²+10x -3000=0
⇒x²+60x-50x-3000=0
⇒x(x+60)-50(x+60)=0
⇒(x+60)(x-50)=0
⇒x= -60,50
∴x=50 [since speed does not negative]
The usually speed of the bus is 50 miles/h.