Answer:
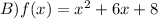
Explanation:
Let
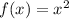 be the parent function. With transformation of function, firstly,we know that,
be the parent function. With transformation of function, firstly,we know that,
- We can move it up or down by adding a constant to the y-value
algebraically
Clearly, The parabola is moved down by 1 unit thus, C is -1. Therefore our function transforms to
secondly, we know that,
- We can move it left or right by adding a constant to the x-value
algebraically,
in case,
- C is positive, g(x) moves to the left and vise versa
Since the parabola is moved left by 3 unit, C is +3, and hence Our function eventually becomes
simplifying it yields:

Hence,B is our required answer