Answer:
Company should produce 8000 phones for the maximum profit.
Explanation:
Function representing cost to the manufacturer is,
C(x) = -21x²+ 67000x + 20006
Function that represents the revenue generated is,
R(x) = -28x² + 179000x
Function representing profit to the company,
Profit = Revenue generated - Cost price
= -28x² + 179000x - (- 21x² + 67000x + 20006)
= -28x² + 21x² + 179000x - 67000x - 20006
P(x) = -7x² + 112000x - 20006
Since this function is a quadratic function therefore, the maximum price generated will be for
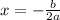
From the given quadratic function, a = (-7), b = 112000 and c = -20006
Therefore, for
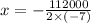
Or x = 8000 the profit to the company will be maximum.
That means pear company should produce 8000 phones for the maximum profit.