Question

30 Points! I need this fast! Thank you

Find the average value of the function g(x) = lnx/x over the interval [1, e].

Answer 1

Explanation:

I don't often see calculus problems here! I like it when I do!

The formula for the average value of a function is

`(1)/(b-a)\int\limits^a_b f({x}) \, dx`

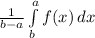
Since e is greater than 1, our lower bound is 1 and the upper is e, and filling in our function we have this integral:

`(1)/(e-1)\int\limits^e_1 {(ln(x))/(x) } \, dx`

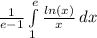
We'll use a u substitution to simplify before we integrate. I teach my calculus students to rewrite the integral identifying what the dx is and therefore, what our du has to "match". For example, the rewrite is:

`(1)/(e-1)\int\limits^e_1 {ln(x)}*(1)/(x) \, dx`

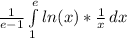
Let u = ln(x), then

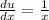`(du)/(dx)=(1)/(x)` and

`du=(1)/(x)dx`

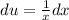
What our du is equal to is the same as what we have designated as our dx in the integral. They "match". So I know I chose the right u. In terms of u, our integral is

`(1)/(e-1)\int\limits^e_1 {u} \, du`

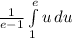
which integrates to
`(u^2)/(2)`

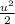
Making the back substitution of ln(x) for u gives us:

`(1)/(e-1)[((lnx)^2)/(2)(1,e)`

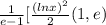
Using the First Fundamental Theorem of Calculus:

`(1)/(1.718281828)[((ln(e))^2)/(2)-((ln(1))^2)/(2)]` which simplifies down to

`(1)/(1.718281828)[(1)/(2)-0]` which finally becomes

`(1)/(3.436563657)=.2909883534`

Round to however many places you need.

Good luck in your calculus class!