Question

A prop for the theater club’s play is constructed as a cone topped with a half-sphere. What is the volume of the prop? Round your answer to the nearest tenth of a cubic inch. Use 3.14 to approximate pi.

Answer 1

The volume of the prop is calculated to be 1,875.6 cubic inches.

Explanation:

Step 1:

The prop consists of a cone and a half-sphere on top. We will have to calculate the volumes of the cone and the half-sphere separately and then add them to obtain the total volume.

Step 2:

The volume of a cone is determined by multiplying
`(1)/(3)` with π, the square of the radius (r²) and height (h). Here we substitute π as 3.14. The radius is 8 inches and the height is 12 inches.

The volume of the cone:
`(1)/(3) \pi r^(2) h = (1)/(3) (3.14) (8^(2)) (12)= 803.84` cubic inches.

Step 3:

The area of a half-sphere is half of a full sphere. The volume of a sphere is given by multiplying
`(4)/(3)` with π and the cube of the radius (r³).

Here the radius is 8 inches. We take π as 3.14.

The volume of a full sphere
`= (4)/(3) \pi r^(3) = (4)/(3) (3.14) (8^(3) ) = 2,143.573` cubic inches.

The volume of the half-sphere
`= (2,143.573)/(2) = 1,071.7865` cubic inches.

Step 4:

The total volume = The volume of the cone + The volume of the half sphere,

The total volume =
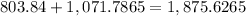`803.84+1,071.7865 = 1,875.6265` cubic inches.

Rounding this off, we get the volume of the prop as 1,875.6 cubic inches.