Question

10 pts!! Multiple choice question (triangles)! Explain how you got your answer!

Answer 1

Option A:

R = 109°

Solution:

Given data:

p = 31 cm, r = 67 cm and ∠P = 26°

To find the measure of angle R.

Using law of sines,

`$(\sin P)/(p)=(\sin R)/(r)`

`$(\sin 26)/(31)=(\sin R)/(67)`

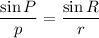
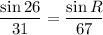
Switch the sides.

`$(\sin R)/(67)=(\sin 26)/(31)`

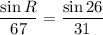
Multiply by 67 on both sides, we get

`$\sin R=(\sin 26)/(31) * 67`

sin R = 0.9474

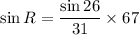
`R= \sin^(-1)0.9474`

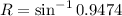
R =71.34 + 360n, 108.65+ 360n, for any integer n

Here R is an obtuse angle, so ignore 71.34.

R = 108.65°

R = 109°

Option A is the correct answer.