Question

A gas that has a volume of 28 liters, a temperature of 42°C, and an unknown pressure has its volume increased to 49 liters and its temperature decreased to 27°C. If the pressure is measured after the change at 4.0 atm, what was the original pressure of the gas?

Answer 1

Hello!

A gas that has a volume of 28 liters, a temperature of 42°C, and an unknown pressure has its volume increased to 49 liters and its temperature decreased to 27°C. If the pressure is measured after the change at 4.0 atm, what was the original pressure of the gas?

We have the following data:

P1 (initial pressure) = ? (in atm)

V1 (initial volume) = 28 L

T1 (initial temperature) = 42ºC (in Kelvin)

TK = TºC + 273.15

TK = 42 + 273.15 → T1 (initial temperature) = 315.15 K

P2 (final pressure) = 4 atm

T2 (final temperature) = 27ºC (in Kelvin)

TK = TºC + 273.15

TK = 27 + 273.15 → T2 (final temperature) = 300.15 K

V2 (final volume) = 49 L

Now, we apply the data of the variables above to the General Equation of Gases, let's see:

`(P_1*V_1)/(T_1) =(P_2*V_2)/(T_2)`

`(P_1*28)/(315.15) =(4*49)/(300.15)`

`(28\:P_1)/(315.15) =(196)/(300.15)`

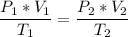
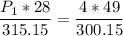
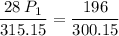
multiply the means by the extremes

`28\:P_1*300.15 = 315.15*196`

`8404.2\:P_2 = 61769.4`

`P_2 = (61769.4)/(8404.2)`

`P_2 = 7.349825087... \to \boxed{\boxed{P_2 \approx 7.35\:atm}}\:\:\:\:\:\:\bf\blue{\checkmark}`

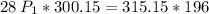
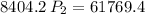
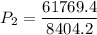
Answer:

The original pressure of the gas is approximately 7.35 atm

_______________________

`\bf\green{I\:Hope\:this\:helps,\:greetings ...\:Dexteright02!}\:\:\ddot{\smile}`

Answer 2

7.35atm

Step-by-step explanation:

Data obtained from the question include:

V1 = 28L

T1 = 42°C = 42 + 273 = 315K

P1 =?

V2 = 49L

T2 = 27°C = 27 + 273 = 300K

P2 = 4atm

Using P1V1/T1 = P2V2/T2, the original pressure can be obtained as follows:

P1V1/T1 = P2V2/T2

P1 x 28/315 = 4 x 49/300

Cross multiply to express in linear form

P1 x 28 x 300 = 315 x 4 x 49

Divide both side by 28 x 300

P1 = (315 x 4 x 49) /(28 x 300)

P1 = 7.35atm

Therefore, the original pressure is 7.35atm