Question

Alex is building a rectangular fence around his yard.The total perimeter of the fence is 68 feet and the area of the yard is 240 square feet. Based on this information, what is the dimensions of the fence?

Answer 1

Therefore the dimensions of the fence 24 feet by 10 feet.

Explanation:

Rectangle

• The opposite sides of a rectangular are congruent
• The opposite angles of a rectangular are congruent
• The area of a rectangular is (length×breadth)
• The perimeter of a rectangular is 2(length+breadth)

Given

The perimeter of the fence is 68 feet

The area of the rectangular yard is 240 square feet

Let the length be x feet and breadth is y feet

According to the problem,

2(length+breadth)=68

⇒2(x+y)=68

⇒
`(x+y)=(68)/(2)`

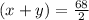
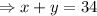`\Rightarrow x+y=34` .......(1)

The area of the rectangular is

length×breadth=240

⇒x×y=240

`\Rightarrow x=(240)/(y)`

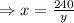
Putting the value x in the equation

`(240)/(y)+y=34`

`\Rightarrow (240+y^2)/(y)=34`

`\Rightarrow 240+y^2=34y`

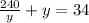
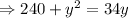
⇒y²-34y+240=0

⇒y²-24y-10y+240=0

⇒y(y-24)-10(y-24)=0

⇒(y-24)(y-10)=0

⇒y=24,10

When, y=24

`x=(240)/(24)=10`

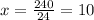
When y=10

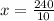`x=(240)/(10)` =24

Therefore the dimensions of the fence 24 feet by 10 feet.