Answer:
The equation representing the scenario is
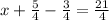 .
.
Explanation:
Given:
Amount of food in the container =
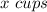
Amount of food added in the container =
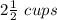
We will now convert the mixed fraction into Improper fraction by Multiplying the whole number part by the fraction's denominator and then add that to the numerator and then write the result on top of the denominator.
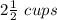 can be rewritten as
can be rewritten as
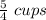
Amount of food added in the container =
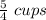
Amount of food removed from container to feed dog =
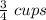
Amount of food remaining =
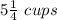
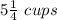 can be Rewritten as =
can be Rewritten as =
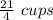
Amount of food remaining =
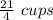
We need to write the equation for above scenario.
Solution:
Now we can say that;
Amount of food remaining is equal to Amount of food in the container plus Amount of food added in the container minus Amount of food removed from container to feed dog.
framing in equation form we get;
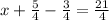
Hence the equation representing the scenario is
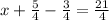 .
.