Answer:
The smart-phone hit the ground when t = 7 s
Explanation:
The height "h" is defined as:
h=16t^2 + 48t + 448
And, when the smart-phone hits the ground, h = 0 ft . Then,
16t^2 + 48t + 448 = 0
And this is a quadratic equation, and we can solve it using the formula for ax^2 + bx + c = 0, which is
x=
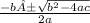
So,
t =
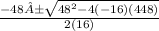
t =
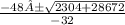
And, we have two responses,
t_1 =
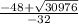 and t_2 =
and t_2 =

t_1 = - 4 s and t_2 = 7 s
As we know, the time is a quantity that cannot have a negative value, so, we take the result 2.