Question

A particle is leaving the Moon in a direction that is radially outward from both the Moon and Earth.

What speed must it have to escape the Moon's gravitational influence?

Express your answer to two significant digits and include the appropriate units.

Answer 1

`2780m/s`

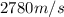
Step-by-step explanation:

Essentially, Kinetic energy of the particle must equal the combined potential energies of earth and the moon when the object is on the moon's surface, meaning the full equation is

`(1)/(2) mv^2=(G(M_E)m)/(r_E) +G(M_mm)/(r_m)\\`

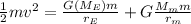
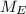`M_E`=Mass of Earth=
`5.97*10^2^4`

`M_m`=Mass of Moon=
`7.4*10^2^2kg`

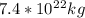
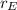`r_E`=distance from earth's center to the moon's=
`3.84*10^8m`

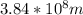
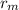`r_m`=radius of moon=
`1.738*10^6m`

After some algebra, the equation simplifies to

`v=\sqrt{2G*((M_E)/(r_E+r_m)+(M_m)/(r_m))}`

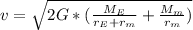
Plugging in the values of G, which is
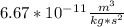`6.67*10^-^1^1 (m^3)/(kg*s^2)`, should yield the proper answer of 2780m/s.