Question

1. A concave mirror has a focal length of 1.50 meters. What is the radius of curvature of the mirror? An object is placed 4.00 meters in front of the mirror. How far in front of the mirror will the image form?

Answer 1

1) 3.0 m

2) 2.40 m

Step-by-step explanation:

1)

A concave mirror is a reflecting surface that causes the reflection of the rays of light coming to the mirror, producing an image of the object facing the mirror.

There are two types of mirror:

- Concave mirror: this is curved inward - as a result, the rays of light coming from the object are reflected back into a single point, called focal point

- Convex mirror: this is curved outward - as a result, the rays of light coming from the object are reflected back into diverging direction, not into a single point

For a curved mirror, the radius of curvature is twice the focal length:

`R=2f`

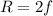
Where

R is the radius of curvature

f is the focal length

In this problem,

f = 1.50 m

So, the radius of curvature is

`R=2(1.50)=3.0 m`

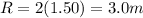
2)

The distance of the image from the mirror can be found by using the mirror equation:

`(1)/(f)=(1)/(p)+(1)/(q)`

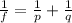
where

f is the focal length

p is the distance of the object from the mirror

q is the distance of the image from the mirror

IN this problem we have:

f = 1.50 m is the focal length

p = 4.00 m is the distance of the object from the mirror

Solving for q, we find:

`(1)/(q)=(1)/(f)-(1)/(p)=(1)/(1.50)-(1)/(4.00)=0.416\\q=(1)/(0.416)=2.40 m`