Explanation:
In trigonometry, the law of sines is an equation that relates the length of the sides of a triangle (any type of triangle) to the sines of its angles. This is expressed mathematically as
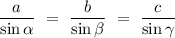 ,
,
where
 ,
,
 , and
, and
 are the lengths of the sides of the triangle and
are the lengths of the sides of the triangle and
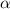 ,
,
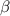 , and
, and
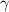 are the opposite angles (as shown in the figure below). Likewise, the law is sometimes written as it reciprocals,
are the opposite angles (as shown in the figure below). Likewise, the law is sometimes written as it reciprocals,
 .
.
Therefore,

Alternatively, you can solve this question using the definition of the trigonometric function sine. For the angle
 in the figure below,
in the figure below,
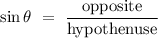 .
.
Therefore,
