Question

A solenoidal coil with 25 turns of wire is wound tightly aroundanother coil with 300 turns. The inner solenoid is 25.0 cm long andhas a diameter of 2.00 cm. At a certain time, the current in theinner solenoid is 0.120 A and is increasing at a rate of1.75x103A/s. For this time, calculate;

a) the average magnetic flux through each turn of the innersolenoid;
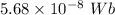
b) the mutual inductance of the two solenoids;
c) the emf induced in the outer solenoid by the changing current inthe inner solenoid
Thanks for any help you can offer! Explanation would be wonderful!

Answer 1

(a). The average magnetic flux through each turn of the inner solenoid is
`5.68*10^(-8)\ Wb`

(b). The mutual inductance of the two solenoids is
`1.183*10^(-5)\ H`

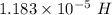
(c). The emf induced in the outer solenoid by the changing current in the inner solenoid is -0.0207 V.

Step-by-step explanation:

Given that,

Number of turns of coil = 25

Number of turns of another coil = 300

Length = 25.0 cm

Diameter = 2.00 cm

Current = 0.120 A

Rate
`(di_(2))/(dt)=1.75*10^(3)\ A/s`

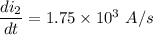
(a). We need to calculate the magnetic field due to inner solenoid

Using formula of magnetic field

`B=\mu_(0)((N_(2))/(l))I`

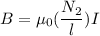
Put the value into the formula

`B=4\pi*10^(-7)*((300)/(0.25))*0.120`

`B=1.81*10^(-4)\ T`

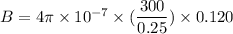
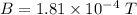
We need to calculate the average magnetic flux through each turn of the inner solenoid

Using formula of magnetic flux

`\phi=B\cdot A`

Put the value into the formula

`\phi=1.81*10^(-4)*\pi* (1.00*10^(-2))^2`

`\phi=5.68*10^(-8)\ Wb`

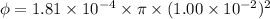
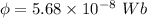
The average magnetic flux through each turn of the inner solenoid is
`5.68*10^(-8)\ Wb`

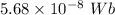
(b). We need to calculate the mutual inductance of the two solenoids

Using formula of mutual inductance

`M=(N_(1)\phi)/(i_(1))`

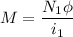
Put the value into the formula

`M=(25*5.68*10^(-8))/(0.120)`

`M=0.00001183\ H`

`M=1.183*10^(-5)\ H`

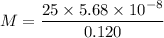
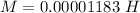
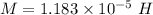
The mutual inductance of the two solenoids is
`1.183*10^(-5)\ H`

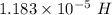
(c). We need to calculate the emf induced in the outer solenoid by the changing current in the inner solenoid

Using formula of emf

`\epsilon=-M(di_(2))/(dt)`

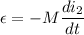
Put the value into the formula

`\epsilon=-1.183*10^(-5)*1.75*10^(3)`

`\epsilon=-0.0207\ V`

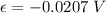
The emf induced in the outer solenoid by the changing current in the inner solenoid is -0.0207 V.

Hence, (a). The average magnetic flux through each turn of the inner solenoid is
`5.68*10^(-8)\ Wb`

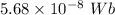
(b). The mutual inductance of the two solenoids is
`1.183*10^(-5)\ H`

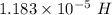
(c). The emf induced in the outer solenoid by the changing current in the inner solenoid is -0.0207 V.