Question

Assume the random variable X is normally distributed with mean muequals50 and standard deviation sigmaequals7. Compute the probability. Be sure to draw a normal curve with the area corresponding to the probability shaded. ​P(54less than or equalsXless than or equals68​) Which of the following normal curves corresponds to ​P(54less than or equalsXless than or equals68​)? A. 545068 A normal curve has a horizontal axis with three labeled coordinates, 50, 54, and 68. The curve's peak is near the top of the graph at horizontal coordinate 50. Three vertical line segments run from the horizontal axis to the curve at 50, 54, and 68. The area under the curve between the vertical line segments at 50 and 54 is shaded. B. 545068 A normal curve has a horizontal axis with three labeled coordinates, 50, 54, and 68. The curve's peak is near the top of the graph at horizontal coordinate 50. Three vertical line segments run from the horizontal axis to the curve at 50, 54, and 68. The area under the curve between the vertical line segments at 54 and 68 is shaded. C. 545068 A normal curve has a horizontal axis with three labeled coordinates, 50, 54, and 68. The curve's peak is near the top of the graph at horizontal coordinate 50. Three vertical line segments run from the horizontal axis to the curve at 50, 54, and 68. The area under the curve to the left of the vertical line segment at 54 is shaded. ​P(54less than or equalsXless than or equals68​)equals nothing ​(Round to four decimal places as​ needed.)

Answer 1

The answers to the questions are as follows;

The probability is 0.27926 and

The correct option is B.

54 50 68 A normal curve has a horizontal axis with three labeled coordinates, 50, 54, and 68. The curve's peak is near the top of the graph at horizontal coordinate 50. Three vertical line segments run from the horizontal axis to the curve at 50, 54, and 68. The area under the curve between the vertical line segments at 54 and 68 is shaded.

Please find the attached normal distribution curve shaded between the z values of 54 and 68.

Explanation:

To solve the question, w calculate the z values as follows

`z = (x-\mu)/(\sigma)`

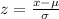
Where:

μ = Mean = 50

σ = Standard deviation = 7

We are asked to draw a normal curve with the area corresponding to the probability P(54 ≤ X ≤ 68) shaded.

On the normal or bell curve, the x axis is the z value, while the y axis is the probability.

Therefore, we have to calculate the z values corresponding to 54 and 68, so we can find them on the normal curve as follows

z value for 54 =
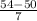`(54-50)/(7)` = 0.571

z value for 68 =
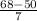`(68-50)/(7)` = 2.571

The probability that 54 is ≤ X and X is ≤ 68 then is obtained from the z value table for the calculated z values and the difference between the two values read from the table is the area under the normal curve bounded by the z value of 54 and 68 which is also the probability.

Therefore probability = area under normal curve between required values

= .99492 - .71566 = 0.27926

We then proceed to draw the normal curve with the other values and place a line at the

• 0 point on the x axis corresponding to the mean = 50

• 0.571 point on the x axis corresponding to first boundary of the area of interest = 54

• 2.571 point on the x axis which is the second boundary of the area of interest = 68.

The area of interest is then shaded and it comes out to be

B. 545068 A normal curve has a horizontal axis with three labeled coordinates, 50, 54, and 68. The curve's peak is near the top of the graph at horizontal coordinate 50. Three vertical line segments run from the horizontal axis to the curve at 50, 54, and 68. The area under the curve between the vertical line segments at 54 and 68 is shaded.