Question

A cup manufacturing company makes small and large snow cone cups with the dimensions shown in the diagram. Which statement

best describes the relationship between the volumes of the cones?
A)
The volume of the large cone is 2 times the volume of the small cone.
B)
The volume of the large cone is 3 times the volume of the small cone.
The volume of the large cone is 3.5 times the volume of the small cone.
D)
The volume of the large cone is 1.5 times the volume of the small cone.

Answer 1

C) The volume of the large cone is 3 times the volume of the small cone.

Explanation:

Step 1:

The volume of a cone is determined by multiplying
`(1)/(3)` with π, the square of the radius (r²) and height (h). Here we substitute π as 3.1415.

The radius of the large cone is 1.5 inches and the height is 4 inches.

The volume of the larger cone
`= (\pi r^(2) h)/(3) = ((3.1415)(1.5^(2) )(4))/(3) = (28.2735)/(3) = 9.4245.`

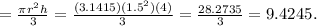
So the volume of the larger cone is 9.4245 cubic inches.

Step 2:

Now, we determine the volume of the small cone.

The radius of the small cone is 1 inch and the height is 3 inches.

The volume of the small cone
`= (\pi r^(2) h)/(3) = ((3.1415)(1^(2) )(3))/(3) = (9.4245)/(3) = 3.1415.`

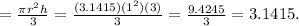
So the volume of the smaller cone is 3.1415 cubic inches.

Step 3:

Now we divide the values on the volume of the large cone by the volume of the small cone.

The volume of the large cone by the volume of the small cone
`= (9.4245)/(3.1415) = 3.`

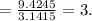
So the volume of the large cone is 3 times the volume of the small cone which is option C.