Question

Assume that females have pulse rates that are normally distributed with a mean of mu equals 72.0 beats per minute and a standard deviation of sigma equals 12.5 beats per minute. Complete parts​ (a) through​ (c) below.

a. If 1 adult female is randomly​ selected, find the probability that her pulse rate is between 66 beats per minute and 78 beats per minute.
The probability is?

b. If 4 adult females are randomly​ selected, find the probability that they have pulse rates with a mean between 66 beats per minute and 78 beats per minute
The probability is?

c. Why can the normal distribution be used in part​ (b), even though the sample size does not exceed​ 30?
A.
Since the mean pulse rate exceeds​ 30, the distribution of sample means is a normal distribution for any sample size.
B.
Since the distribution is of sample​ means, not​ individuals, the distribution is a normal distribution for any sample size.
C.
Since the original population has a normal​ distribution, the distribution of sample means is a normal distribution for any sample size.
D.
Since the distribution is of​ individuals, not sample​ means, the distribution is a normal distribution for any sample size.

Answer 1

the answer would be C

Answer 2

a) 36.88% probability that her pulse rate is between 66 beats per minute and 78 beats per minute

b) 66.30% probability that they have pulse rates with a mean between 66 beats per minute and 78 beats per minute

c)

C.

Since the original population has a normal​ distribution, the distribution of sample means is a normal distribution for any sample size.

Explanation:

To solve this question, we need to understand the normal probability distribution and the central limit theorem.

Normal probability distribution:

Problems of normally distributed samples are solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

Central limit theorem:

The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean
`\mu` and standard deviation
`\sigma`, the sample means with size n of at least 30 can be approximated to a normal distribution with mean
`\mu` and standard deviation
`s = (\sigma)/(√(n))`

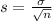
In this problem, we have that:

`\mu = 72, \sigma = 6.5`

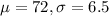
a. If 1 adult female is randomly​ selected, find the probability that her pulse rate is between 66 beats per minute and 78 beats per minute.

The probability is?

This is the pvalue of Z when X = 78 subtracted by the pvalue of Z when X = 66. So

X = 78

`Z = (X - \mu)/(\sigma)`

`Z = (78 - 72)/(12.5)`

`Z = 0.48`

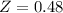
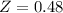`Z = 0.48` has a pvalue of 0.6844

X = 66

`Z = (X - \mu)/(\sigma)`

`Z = (66 - 72)/(12.5)`

`Z = -0.48`

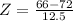
`Z = -0.48` has a pvalue of 0.3156

0.6844 - 0.3156 = 0.3688

36.88% probability that her pulse rate is between 66 beats per minute and 78 beats per minute

b. If 4 adult females are randomly​ selected, find the probability that they have pulse rates with a mean between 66 beats per minute and 78 beats per minute

The probability is?

Now we have
`n = 4, s = (12.5)/(√(4)) = 6.25`

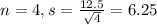
So

X = 78

`Z = (X - \mu)/(\sigma)`

By the Central Limit Theorem

`Z = (X - \mu)/(s)`

`Z = (78 - 72)/(6.25)`

`Z = 0.96`

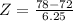
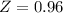
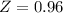`Z = 0.96` has a pvalue of 0.8315

X = 66

`Z = (X - \mu)/(s)`

`Z = (66 - 72)/(6.25)`

`Z = -0.96`

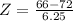
`Z = -0.96` has a pvalue of 0.1685

0.8315 - 0.1685 = 0.6630

66.30% probability that they have pulse rates with a mean between 66 beats per minute and 78 beats per minute

c. Why can the normal distribution be used in part​ (b), even though the sample size does not exceed​ 30?

The condition for the sample size exceeding 30 is when the population is skewed. If it is normally distributed, the size is not a condition.

So the correct answer is:

C.

Since the original population has a normal​ distribution, the distribution of sample means is a normal distribution for any sample size.