Question 1
The given system of equations is:
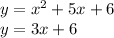
Equate the two equations:
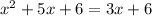
Rewrite in standard form:

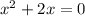
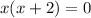

When we put x=0, in y=3x +6, we get:
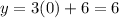
One solution is (0,6)
When we put x=-2, into y=3x+6, we get:
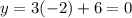
Another solution is (-2,0)
The solutions are; (0,6) and (-2,0)
Question 2:
The function is

Let us put x=-x,
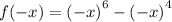
This gives:
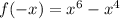
We can observe that:
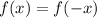
This is the property of an even function.
Question 3:
The given function is
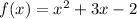
The average rate of change of f(x) from x=a to x=b is given as:
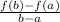
This is the slope of the secant line connecting the two points on f(x)
From x=2 to x=6, the average rate of change
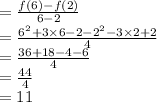
The average rate of change is 11