Step-by-step explanation:
It is given that
 for acetic acid is
for acetic acid is
 . And, its
. And, its
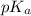 value will be calculated as follows.
value will be calculated as follows.
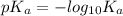
=
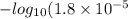
= 4.74
And, according to the Henderson-Hasselbalch equation,
pH =
![pK_(a) + log ([Salt])/([Acid])](https://img.qammunity.org/2021/formulas/chemistry/college/iu4z7vaoa6pmftlfe2qyrxgmkrii8iaq26.png)
(1). When [Acetic acid] is ten times greater than [acetate]
This means that
![\frac{[\text{Acetate}]}{[\text{Acetic acid}]} = (1)/(10)](https://img.qammunity.org/2021/formulas/chemistry/college/v2zk3h61599hpsd3qjqpqvlhwyaocasxyy.png)
So, pH =
![pK_(a) + log \frac{[Acetate]}{[\text{Acetic Acid}]}](https://img.qammunity.org/2021/formulas/chemistry/college/5hg8u0kju3nnvns2cuqqrerij4a5z0em1s.png)
=
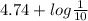
= 3.74
(2). When [Acetate] ten times greater than [Acetic acid]
This means that
![\frac{[Acetate]}{\text{Acetic acid}}](https://img.qammunity.org/2021/formulas/chemistry/college/cnmwcktk2k6g5wgjfsfxg2ruouxunudwfz.png) =
=
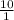
pH =
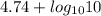
= 5.74
(3). When [acetate] = [acetic acid]
This means that
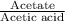 = 1
= 1
pH =
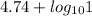
= 4.74