zeros of the function y=
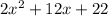 is
is
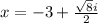 &
&
 .
.
Explanation:
Here we have , y=
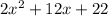 in order to find zeros of this quadratic function we get:
in order to find zeros of this quadratic function we get:
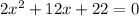
⇒
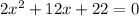
⇒
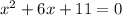
⇒
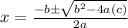
⇒
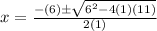
⇒
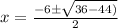
⇒
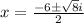
⇒
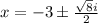
Since, we have two root one with positive & other with negative sign so :
⇒

Therefore, zeros of the function y=
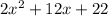 is
is
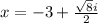 &
&
 .
.