Question

A pumpkin is launched from the top of a 20 foot tall platform at an initial velocity of 84 feet per second. The height, h, of the pumpkin at time t seconds after the launch can be modeled by the equation h(t) = −16t 2 + 84t + 20. Find the maximum height reached by the pumpkin

Answer 1

Step-by-step explanation:

In this problem we have a pumpkin is launched from the top of a 20 foot tall platform at an initial velocity of 84 feet per second. So the height, h, of the pumpkin at time t seconds after the launch can be modeled by the equation:

`h(t) = -16t^2 + 84t + 20`

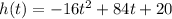
So this is the equation of a parabola. The maximum of this parabola occurs at its vertex. So let's find this vertex:

`\text{The x-value of the vertex is}: \\ \\ t=-(b)/(2a) \\ \\ \\ Where: \\ \\ a=-16 \\ \\ b=84 \\ \\ c=20 \\ \\ \\ t=-(84)/(2(-16)) \\ \\ t=-(84)/(-32) \\ \\ t=(21)/(8)=2.625 \\ \\ h(2.625)=-16(2.625)^2+84(2.625)+20 \\ \\ h(2.625)=-110.25+220.5+20 \\ \\ h(2.625)=130.25m`

Finally, the maximum occurs at time 2.625 seconds when the height is 130.25m