Question

Which point is on the circle whose equation is x^2 + y^2 = 289

1) (-12,12) 2) (7,-10) 3) (-1,-16) 4) (8,-15)

Answer 1

Point 4) (8, -15) is on the circle.

Explanation:

Step 1:

To determine which point lies on the circle equation, we substitute the different x and y values in the equation and check to see which best satisfies the values in the equation.

The equation of the circle is
`x^(2) +y^(2) = 289.`

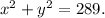
Step 2:

When
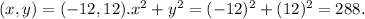`(x,y) = (-12,12). x^(2) +y^(2) = (-12)^(2) + (12)^(2) = 288.` 288 ≠ 289.

When
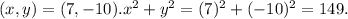`(x,y) = (7,-10). x^(2) +y^(2) = (7)^(2) + (-10)^(2) = 149.` 149 ≠ 289.

When
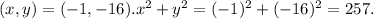`(x,y) = (-1,-16). x^(2) +y^(2) = (-1)^(2) + (-16)^(2) = 257.` 257 ≠ 289.

When
`(x,y) = (8,-15). x^(2) +y^(2) = (8)^(2) + (-15)^(2) = 289.`

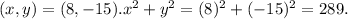
So the fourth set of values is on the circle.