Question

How do you writer this function in standard form??

Answer 1

Question 1) Function defining the table:

From the table the x-intercepts are -2 and 1. This means the factors are:

(x+2) and (x-1)

Let

`h(x) = a(x + 2)(x - 1)`

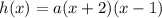
The point (-1,-1) satisfy this function since it is from the same table.

`- 1 = a( - 1 + 2)( - 1 - 1) \\ - 1 = - 2a \\ a = (1)/(2)`

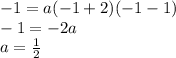
Therefore the function is

`h(x) = (1)/(2) (x + 2)(x - 1)`

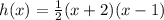
We expand to get:

`h(x) = (1)/(2) ( {x}^(2) + x - 2)`

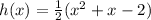
The standard form is:

`h(x) = \frac{ {x}^(2) }{2} + (x)/(2) - 1`

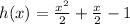
Question 3) Parabola opening up

The x-intercepts are x=3 and x=7

The factors are (x-3), (x-7)

The factored from is

`y = a(x - 3)(x - 7)`

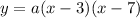
The curve passes through (5,-4)

`- 4= a( 5- 3)( 5 - 7) \\ - 4= - 4a \\ a = 1`

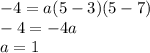
The equation is:

`y = (x - 3)(x + 7)`

Expand:

`y = {x}^(2) + 7x - 3x - 21`

`y = {x}^(2) + 4x - 21`

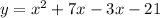
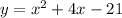
This is the standard form:

Question 3) Parabola opening down:

The x-intercepts are x=-5 and x=1

The factors are (x+5), (x-1)

The factored form is

`y = - (x + 5)(x - 1)`

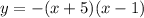
We expand to get:

`y = - ( {x}^(2) - x + 5x - 5)`

`y = - {x}^(2) - 4x + 5`

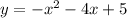
This is the standard form.