Question

A marketing company wants to estimate the proportion of consumers in a certain region of the country who would react favorably to a new marketing campaign. Further, the company wants the estimate to have a margin of error of no more than 5 percent with 90 percent confidence. Of the following, which is closest to the minimum number of consumers needed to obtain the estimate with the desired precision?a. 136

b. 271
c. 385
d. 542
e. 769

Answer 1

The closest to the minimum number of consumers needed to obtain the estimate with the desired precision is (b) 271

Step-by-step explanation:

When the prior estimate of population proportion is not given , then the formula to find the sample size is given by :-

`n=0.25((z^(*) )/(E) )^(2)`

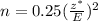
where E = Margin of error.

z* = Critical z-value.

As per given , we have

E = 5%=0.05

Confidence level = 90%

The critical value of z at 90% is 1.645 (By z-table)

Put all values in the formula , we get

n=0.25(1.645/0.05)²

n=0.25(32.9)²

n=270.6025≈271

Thus, the minimum sample size needed = 271

Hence , the correct answer is 271 .