Answer:
2000 years
Step-by-step explanation:
A radioactive molecule will continuously decay and turn into another molecule. This nature of the radioactive molecule makes them can be used to estimate the age of an object. Half-life is the unit of time needed for radioactive molecules to decay to half of its mass. The formula for the mass remaining will be:
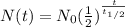
Where
N(t)= number of the molecule remains
N0= number of molecule initially
t= time elapsed
t1/2= half time
We have all variable besides the half time, the calculation will be:
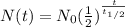
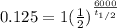
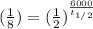

3= 6000/ (t1/2)
t1/2= 6000/3= 2000
The half-life is 2000 years