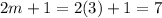Question

A diffraction grating with 600 lines/mmlines/mm is illuminated with light of wavelength 510 nmnm. A very wide viewing screen is 4.6 mm behind the grating. Part A What is the distance between the two mm

Answer 1

A.2.95 m

B.7

Step-by-step explanation:

We are given that

Diffraction grating=600 lines/mm

d=
`(1 mm)/(600)=(1* 10^(-3) m)/(600)=1.67* 10^(-6) m`

Wavelength of light,
`\lambda=510 nm=510* 10^(-9) m`

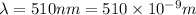
l=4.6 m

A.We have to find the distance between the two m=1 bright fringes

`sin\theta=(m\lambda)/(d)`

For first bright fringe, =1

`sin\theta=(1* 510* 10^(-9))/(1.67* 10^(-6))=0.305`

`\theta=sin^(-1)(0.305)=17.76^(\circ)`

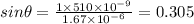
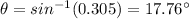
The distance between two m=1 fringes

`x=2ltan\theta=2* 4.6 tan(17.76^(\circ))=2.95 m`

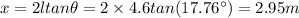
Hence, the distance between two m=1 fringes=2.95 m

B.For maximum number of fringes,

`sin\theta=1`

`sin\theta=(m\lambda)/(d)`

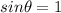
Substitute the values

`1=(m* 510* 10^(-9))/(1.67* 10^(-6))`

`m=(1.67* 10^(-6))/(510* 10^(-9))=3.3\approx 3`

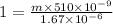
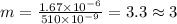
Maximum number of bright fringes on the scree=
`2m+1=2(3)+1=7`