Question

What is the approximate difference in the growth rate of the two populations?

Answer 1

B

Explanation:

The approximate difference in the growth rate is 40 percent.

Answer 2

The approximate difference in the growth rate of the two populations is 40%.

Explanation:

The complete question is

The graph shows the population of deer for the past 5 years. what is the approximate difference in the growth rate of the two populations?​

The picture of the question in the attached figure

we know that

The equation of a exponential growth function is given by

`y=a(1+r)^x`

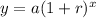
where

y is the population

x is the number of years

a is the initial value

r is the growth rate

step 1

Find the equation of the red curve

we have

`a=10` ---> value of y when the value of x is equal to zero

substitute

`y=10(1+r)^x`

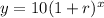
we have the point (2,22.5)

substitute the value of x and the value of y in the equation

`22.5=10(1+r)^2`

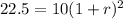
solve for r

`2.25=(1+r)^2`

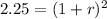
square root both sides

`1+r=1.5\\r=1.5-1\\r=0.5`

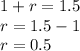
therefore

The growth rate of red curve is 0.50 or 50%

step 2

Find the equation of the blue curve

we have

`a=10` ---> value of y when the value of x is equal to zero

substitute

`y=10(1+r)^x`

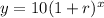
we have the point (7,19.4)

substitute the value of x and the value of y in the equation

`19.4=10(1+r)^7`

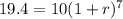
solve for r

`1.94=(1+r)^7`

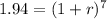
elevated both side to 1/7

`1+r=\sqrt[7]{1.94}`

`r=1.10-1\\r=0.10`

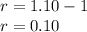
therefore

The growth rate of red curve is 0.10 or 10%

step 3

Find the approximate difference in the growth rate of the two populations

Subtract the two growth rate

`50-10=40\%`

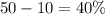
Therefore

The approximate difference in the growth rate of the two populations is 40%.