Answer:
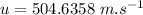 is the initial velocity of the bullet.
is the initial velocity of the bullet.
Step-by-step explanation:
Given:
- mass of the bullet,
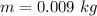
- final velocity of the bullet,
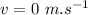
- mass of the wooden block,
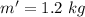
- initial velocity of the block,
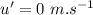
- coefficient of friction between the block and the surface,
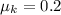
- displacement of the block on the surface due to impact,
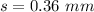
Since here there is no mention of the penetration by the bullet therefore we consider the bullet to be a point that sticks on the surface of the block as soon as it collides.
From the conservation of linear momentum:
Momentum of the system just before collision = momentum of the system just after collision
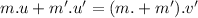
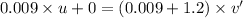 .............................(1)
.............................(1)
where:
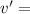 final velocity of the combined mass of block and bullet
final velocity of the combined mass of block and bullet
Now the frictional force will be due to combined mass:
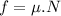
where:
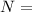 normal reaction from the surface due to weight
normal reaction from the surface due to weight
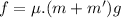
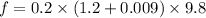
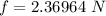 This is the force that brings deceleration in the combined mass.
This is the force that brings deceleration in the combined mass.
Now the deceleration rate:
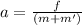
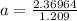
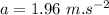 Since the force of friction acts in the opposite direction so this acceleration will also act in the same direction.
Since the force of friction acts in the opposite direction so this acceleration will also act in the same direction.
Now using the equation of motion for the course of motion when the masses just combine after collision:
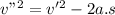
(using -ve sign because the acceleration opposes the motion here)
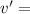 initial velocity of the combined mass just after collision
initial velocity of the combined mass just after collision
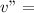 final velocity of the combined mass = 0
final velocity of the combined mass = 0
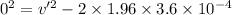
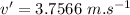
Now using eq. (1):
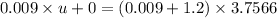
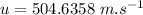 is the initial velocity of the bullet.
is the initial velocity of the bullet.