Answer:
Part 1)
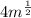
Part 2)
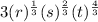
Part 3)
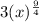
Explanation:
Part 1) Write each expression without the radical.
we have
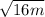
we know that
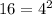
substitute
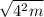
Remember that
![\sqrt[a]{x^b}=x^{(b)/(a)}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/yf05zcldd8vt44x7ttyi9c1kx59iwa8tq8.png)
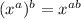
so
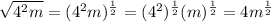
Part 2) Write each expression without the radical.
we have
![\sqrt[3]{27rs^2t^4}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/ft20thx40s67gmvvyazo9qxdhi4q501g2p.png)
we know that
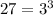
substitute
![\sqrt[3]{3^3rs^2t^4}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/owq7y6f0ke7x2rs8yujbtpp9imcm7hx2zh.png)
Remember that
![\sqrt[a]{x^b}=x^{(b)/(a)}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/yf05zcldd8vt44x7ttyi9c1kx59iwa8tq8.png)
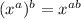
so
![\sqrt[3]{3^3rs^2t^4}=(3^3rs^2t^4)^{(1)/(3)}=(3^3)^{(1)/(3)}(r)^{(1)/(3)}(s^2)^{(1)/(3)}(t^4)^{(1)/(3)}=3(r)^{(1)/(3)}(s)^{(2)/(3)}(t)^{(4)/(3)}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/jvjfrk1cihuk8bg2sepjg1vedph80yrljw.png)
Part 3) Write each expression without the radical.
we have
![\sqrt[4]{81x^9}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/kbx3w9q7e2gf9q8co18buc9umh3bx7uabw.png)
we know that
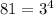
substitute
![\sqrt[4]{3^4x^9}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/jjoqqf3ea9gx5nlfdgt81lppw6h5qs2k9h.png)
Remember that
![\sqrt[a]{x^b}=x^{(b)/(a)}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/yf05zcldd8vt44x7ttyi9c1kx59iwa8tq8.png)
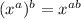
so
![\sqrt[4]{3^4x^9}=(3^4x^9)^{(1)/(4)}=(3^4)^{(1)/(4)}(x^9)^{(1)/(4)}=3(x)^{(9)/(4)}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/k9s66e2j21acw6r84s4vyto2n5cn18nrxi.png)