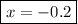Question

Find x for,
sin⁻¹ 4x + sin⁻¹ 3x = -
`(\pi )/(2)`

Answer 1

Step-by-step explanation:

Let's solve this problem graphically. Here we have the following equation:

`sin^(-1)(4x) + sin^(-1)(3x) = -(\pi)/(2)`

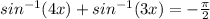
So we can rewrite this as:

`f(x)=sin^(-1)(4x) + sin^(-1)(3x) \\ \\ g(x)= -(\pi)/(2)`

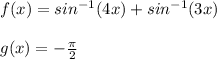
So the solution to the equation is the x-value at which the functions f and g intersect. In other words:

`f(x)=g(x) \\ \\ sin^(-1)(4x) + sin^(-1)(3x) = -(\pi)/(2)`

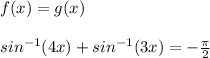
Using graphing calculator, we get that this value occurs at:

`\boxed{x=-0.2}`