Question

Q6. Sakira invested £3550 in a savings account for 3 years.

She was paid 2.6% per annum compound interest for each of the first 2 years,
She was paid R% interest for the third year,
Sakira had £3819.21 in her savings account at the end of the 3 years.
Work out the value of R.
Give your answer correct to 1 decimal place.

Answer 1

Answer:2.2

Explanation:

Answer 2

2.2%

Explanation:

Given the initial invested as £3550, compound interest rate for first two years as 2.6% and interest for third year as R% and a final amount as £3819.21, R% can be calculated as:

#Compound interest in first two years:

`A=P(1+i)^n, p=\£3550, i=2.6\%, n=2\\\\A=£3550(1.026)^2\\\\A=3737.00`

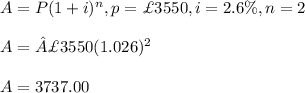
#Hence, the total amount after first two years is £3737. To find R%, we further compound it for the final year and equate it to the final amount:

`A=P(1+I)^n, A=\£3819.21,i=R\%, n=1, P=\£3737\\\\3819.21=3737(1+i)\\\\(1+i)=(3819.21)/(3737)\\\\i=(3819.21)/(3737)-1\\\\i=1.021999-1\\\\i=0.02199`

Hence, R% is equivalent to 2.2%