Question

Use synthetic substitution to find f(­2) and f(3).

1.f(x) = 3x^4 ­- 12x^3 ­- 12x^2 + 30x

2. Write the polynomial equation of degree 4 with leading coefficient 1 that has roots at ­-2, ­-1, 3, and 4.

Answer 1

see explanation

Explanation:

(1)

To obtain f(2) and f(3) substitute x = 2, x = 3 into f(x)

f(2) = 3(
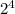`2^(4)` ) - 12(2³) - 12(2²) + 30(2)

= 48 - 96 - 48 + 60 = - 36

f(3) = 3(
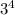`3^(4)` ) - 12(3³) - 12(3²) + 30(3)

= 243 - 324 - 108 + 90 = - 99

(2)

Given a polynomial with roots x = a, x = b, then

(x - a), (x - b) are the factors

and the polynomial is the product of the factors

Here the roots are x = - 2, x = - 1, x = 3 and x = 4, thus the factors are

(x + 2), (x + 1), (x - 3) and (x - 4)

The polynomial is the product of the factors, thus

f(x) = (x + 2)(x + 1)(x - 3)(x - 4) ← expand in pairs using FOIL

= (x² + 3x + 2)(x² - 7x + 12) ← distribute

=
`x^(4)` - 7x³ + 12x² + 3x³ - 21x² + 36x + 2x² - 14x + 24 ← collect like terms

=
`x^(4)` - 4x³ - 7x² + 22x + 24