Question

Gas has a volume of 247.3 ML and is at 100 Celsius and 745MM HG. If the mass of the gas is 0.347G what is the molar mass of the vapor

Answer 1

Answer: The molar mass of the vapor comes out to be 43.83 g/mol. This problem is solved by using ideal gas equation. The ideal gas equation is shown below

`\textrm{PV} =\textrm{nRT}`

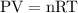
Step-by-step explanation:

Volume of gas = V = 247.3 mL

V = 0.2473 L

Pressure of gas = P = 745 mmHg

1 atm = 760 mmHg

`\textrm{P} = \displaystyle (745)/(760) \textrm{ atm} = 0.98026 \textrm{ atm}`

Temperature of gas = T = 100
`^(\circ)C` = 373 K

Given mass of gas = m = 0.347 g

Assuming molar mass of gas to be M g/mol

Assuming the gas to be an ideal gas, the ideal gas equation is shown below

`\textrm{PV} =\textrm{nRT}`

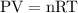
Here, n is the number of moles of gas and R is the universal gas constant.

`\textrm{PV} =\textrm{nRT} \\\textrm{PV} = \displaystyle (m)/(M)\textrm{RT} \\0.98026 \textrm{ atm}* 0.2473 \textrm{ L} = \displaystyle \frac{0.347 \textrm{ g}}{M}* 0.0821 \textrm{ L.atm.mol}^(-1).K^(-1)* 373 \textrm{ K} \\M = 43.83 \textrm{ g/mol}`

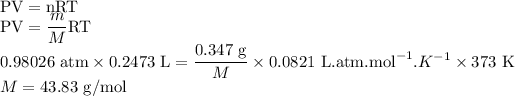
Hence, the molar mass of the vapor comes out to be 43.83 g/mol